揭秘正割函数:三角世界的神秘力量
亲爱的数学探索者,你是否曾在学习三角函数时,对那个看似神秘又充满魅力的正割函数(sec函数)感到好奇?今天,就让我们一起揭开这层神秘的面纱,探索正割函数的奥秘吧!
一、正割函数的诞生
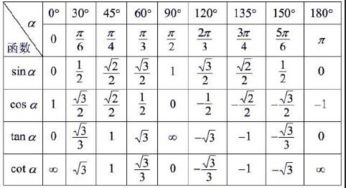
正割函数,简称sec函数,是三角函数家族中的一员。它起源于古老的数学世界,最早可以追溯到古希腊时期。在直角三角形中,正割函数代表着斜边与邻边的比值。简单来说,如果你有一个直角三角形,想知道斜边长度,只需知道一个锐角和邻边长度,正割函数就能帮你算出斜边长度。
二、正割函数的公式与性质
正割函数的公式是:sec(θ) = 1/cos(θ),其中θ代表角度,cos(θ)代表余弦函数。这个公式告诉我们,正割函数是余弦函数的倒数。有趣的是,正割函数与余弦函数的关系不仅仅如此,它们在图像上也有着密切的联系。
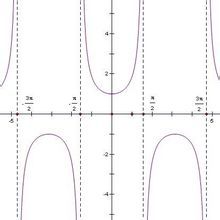
正割函数的图像具有以下特点:
1. 周期性:正割函数是一个周期函数,周期为2π。这意味着,每隔2π,正割函数的图像就会重复一次。
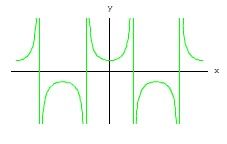
2. 间断点:正割函数在余弦函数的零点处(即cos(θ) = 0)存在间断点。这些点分别是θ = π/2 kπ,其中k为整数。
3. 渐近线:正割函数在y = 1和y = -1处存在渐近线。这些渐近线是正割函数图像的重要特征。
4. 单调性:在(0, π/2)和(3π/2, 2π)区间内,正割函数是递增的;在(π/2, 3π/2)区间内,正割函数是递减的。
三、正割函数的应用
正割函数在数学、物理、工程等领域有着广泛的应用。以下是一些常见的应用场景:
1. 物理学:在振动学中,正割函数可以用来描述振动系统中某一点的位移随时间的变化关系。
2. 工程学:在电路分析中,正割函数可以用来计算电路的阻抗。
3. 天文学:在天体物理学中,正割函数可以帮助计算天体的位置和距离。
4. 数学分析:在数学分析领域,正割函数的性质和图像是研究函数性质、积分和微分的重要工具。
四、正割函数的拓展
正割函数不仅限于直角三角形,还可以扩展到复数领域。在复数域中,正割函数可以表示为sec(z) = (e^(iz) e^(-iz)) / 2,其中z为复数。
五、
正割函数,这个看似神秘的三角函数,其实在我们的生活中有着广泛的应用。通过本文的介绍,相信你已经对正割函数有了更深入的了解。在未来的数学探索中,希望你能继续关注这个有趣的函数,发现更多它的奥秘。加油,数学小勇士!
